Filtro adaptado

0. Introducción

El problema que pretendemos solucionar es la transmisión de una información mediante unas formas de onda desde el emisor al receptor. Todas las explicaciones de este documento están referidas a comunicación en banda base, aunque se podría generalizar a señales moduladas. Empezaremos utilizando pulsos rectangulares con anchura B (su ancho de banda) y veremos por qué no nos sirven ese tipo de pulsos, haciendo sucesivos comentarios acerca de posibles mejoras a lo largo de todo el canal de comunicación.

1. Interferencia entre símbolos (ISI)

Al emplear pulsos rectangulares en frecuencia, éstos en el tiempo se traducen en funciones sinc, con pasos por cero cada T=1/2B. Esta función sinc tiene una serie de lóbulos secundarios que, si el instante de muestreo no es lo suficientemente perfecto, en esos casos no sólo se va a detectar la parte de señal correspondiente al bit o símbolo que nos interesa, sino que también se estará detectando superpuesto a lo anterior una parte de bit correspondiente a algún bit o símbolo contíguo (es decir, se produce ISI). Al final, la conjunción de la ISI, el efecto del ruido y otras interferencias pueden llevarnos a recibir un símbolo erróneo.

La solución que se plantea para evitar en cierto modo el problema anterior es la utilización de una señal cuya respuesta en frecuencia sea el coseno alzado, que en el dominio del tiempo también tiene pasos por cero cada T, siendo sus lóbulos secundarios de menor significancia que en el caso de la señal rectangular, y además presenta pasos por cero intermedios entre cero y cero que presentaba la señal rectangular. El único problema de la señal en coseno alzado es que ocupa el doble de ancho de banda (permite tan solo la mitad del bit rate de los pulsos rectangulares).

2. La familia del coseno alzado

Existe una familia de señales con respuesta frecuencial en coseno alzado. Cada una de ellas tiene un factor de roll-off diferente, que va a acondicionar el ancho de banda y la respuesta impulsional. El factor de roll-off indica el porcentaje de ancho de banda que excede la señal de la familia del coseno alzado respecto ancho de banda que ocuparía el pulso rectangular cuya respuesta impulsional presentara los mismos pasos por cero. De este modo, la señal explicada en el apartado anterior correspondería a un roll-off del 100%, una señal con un roll-off del 50% tendría un ancho de banda un 50% más grande que la rectangular correspondiente y una rectangular pura se correspondería con un factor de roll-off del 0%. El coseno alzado con roll-off del 100%, a pesar de ser la de mayor ancho de banda, presenta una gran ventaja en el dominio del tiempo, ya que además de los pasos de cero que ya presentaba la rectangular, añade unos nuevos pasos por cero justo en la mitad de cada intervalo, que son muy prácticos para establecer sincronismos y generar los relojes en el receptor.

El elegir uno u otro roll-off dependerá de varios factores, como la disponibilidad de ancho de banda, los niveles de ruido esperados, el bit rate deseado, etc. Así por ejemplo, el CCITT establece un roll-off del 75% para el módem V.22 bis, mientras que en algunos sistemas de radio digital por satélite se usan factores de roll-off del 30%.

Pero esto no es tan fácil y bonito como parece, porque el pulso recibido va a depender del pulso transmitido, del canal y del receptor, y las características del canal no se van a poder modificar y además variarán contínuamente por varias circunstancias.

3. Diagramas de ojo

Son la representación en un osciloscopio de la señal recibida (en el dominio del tiempo, claro está). En estos diagramas se representan los intervalos de todos y cada uno de los bits recibidos, y su mayor o menor claridad en la representación nos dará una idea de la mejor o peor calidad de la transmisión.

4. Ecualización digital

Si enviamos un único pulso rectangular desde el emisor, cuya respuesta impulsional es la famosa sinc con sus famosos pasos por cero cada T, es posible que en recepción esos pasos por cero se hayan movido un poquillo debido al ruido o a alguna interferencia y en vez de ser un cero sea un valor próximo a cero pero no nulo. Para evitar éso se pone en recepción un ecualizador que fuerce los pasos por cero. Estos filtros consistirán básicamente en unos coeficientes que serán los correspondientes a las muestras de la señal con la que convolucionemos la entrada para obtener la señal deseada. 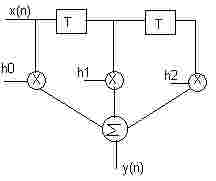Una de las ventajas de utilizar un ecualizador digital de este tipo es que los mencionados coeficientes se pueden adaptar a las características del canal: si se transmite un pulso "de entrenamiento" conocido y se muestrea a la salida, a partir de la salida obtenida se pueden obtener dichos coeficientes. Desafortunadamente las características del canal suelen fluctuar. Es necesario entonces implementar algún algoritmos mediante el cual se recalculen dichos coeficientes tras emitir el pulso "de entrenamiento" de vez en cuando. A esta técnica se le conoce como ecualización adaptativa. En la figura se observa la forma que debería tener uno de éstos filtros, siendo los h0, h1 y h2 sus coeficientes.

5. Ortogonalidad

Se dice que dos señales son ortogonales si la integral del producto de ambas señales (en el dominio del tiempo) es cero, por lo que también su correlación va a ser cero. De ese modo, dos pulsos rectangulares en intervalos de tiempo diferentes (por ejemplo el primero de o a T y el segundo de T a 2T) son ortogonales: su correlación es nula. Por otro lado la correlación de una señal consigo misma (autocorrelación) nos va a dar idea de la energía de esa señal (la autocorrelación es el límite cuando T tiende a infinito de 1/T de la energía de la señal). Debido a la ortogonalidad y lo relativo a la energía, si transmitimos una señal que es superposición de dos señales s1 y s2, ambas ortogonales entre sí, la energía de dicha señal (elevando la suma de ambas al cuadrado) va a ser la suma de las energías de cada una de ellas, ya que al ser ambas señales ortogonales, las componentes cruzadas se van a eliminar.

6. Detección mediante filtro adaptado

Si origináramos nuestras señales en función de unos pulsos básicos que fueran ortogonales entre sí, podríamos realizar la detección de las señales mediante la correlación, decidiendo qué simbolo se recibe en presencia de ruido. 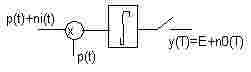Esto se consigue símplemente multiplicando la señal recibida por cada uno de los pulsos básicos y realizando la integral de eso. Si no existiera ruido el resultado sería cero si dicha señal coincide con la enviada. En presencia de ruido sin embargo, todas las integrales van a ser no nulas, aunque sólo una de las integrales tendrá un valor apreciable, siendo su pulso correspondiente la señal que estimaremos como la enviada. La contribución del ruido a estas integrales va a ser prácticamente nula.

Este receptor mediante correlación puede ser cambiado por un proceso de filtrado si conseguimos que la salida de tal filtro ante un pulso determinado sea igual a la energía del pulso. Si conseguimos un filtro de estas características que sea lineal, entonces lo podremos modelar en el dominio del tiempo por su respuesta impulsional o en frecuencia por su respuesta frecuencial. Para que la convolución del pulso recibido por el filtro, p(t), con la respuesta impulsional del filtro, h(t) sea la energía de p(t), h(t) debería ser p(T-t), ( la convolución implica invertir h(t), multiplicar éso por p(t) e ir desplazando h(-t) en el tiempo). En frecuencia se va a verificar que el módulo de H y de P son los mismos, y que Arg(H(w)) = -wT - Arg(P(w)). Por las características del módulo de la respuesta frecuencial, el filtro suprimirá todas las frecuencias que no estén presentes en P(w). Por otra parte, de la expresión de la fase se observa que el filtro tiende a desplazar las fases de las componentes frecuenciales al instante T, que es precisamente el instante de muestreo. Las componentes del ruido, si este es aleatorio blanco y gaussiano (AWGN) con media cero, al tener fases aleatorias, tienden a ser canceladas (además del ruido que queda fuera de la banda ocupada por H(w)).

Si a la entrada del filtro adaptado tenemos un ruido AWGN de media cero, el ruido a la salida seguirá siendo gaussiano, aunque ya no será blanco, y su potencia será EN/2, siendo E la energía del pulso y N (eta) la densidad espectral de potencia del ruido de entrada. Al ser el ruido a la salida del filtro gaussiano, la función Q puede servirnos para determinar la probabilidad de error. En el instante T la señal deseada es numéricamente igual a E, y la desviacion estándar del ruido de salida es \/¯EN/2. Por todo ello, la probabilidad de error es Pe = Q [señal de pico/2 * desviación estándar ]. Pe=Q[\/¯E/2N].

El significado de esa fórmula es que, si empleamos un filtro adaptado, para cualquier pulso empleado la probabilidad de error vendrá determinado únicamente or la energía del pulso y por la densidad espectral de potencia del ruido. Además, para mejorar la probabilidad de error no es suficiente con variar la forma del pulso, manteniendo su energía constante. Deben añadirse mejoras adicionales, como una aproximación a un detector óptimo o una reduccion de la ISI. Por el contrario, si la forma del pulso debe ser alterada por alguno de esos propósitos, el BER no tiene por que verse modificado si empleamos el mismo detector óptimo y la energía del pulso es la misma.

Pero aún no ha quedado muy claro de en qué momento del sistema de comunicaciones debe aparecer el pulso en forma de coseno alzado, ya que si éste se generara en el emisor, podría llegar distorsionado en la recepción. Si suponemos un canal ruidoso con ruido blanco (densidad espectral plana), el espectro de la señal recibida tendrá la forma GT(f)GR(f).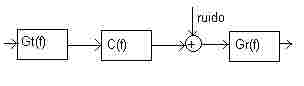Por otra parte, si usamos un receptor óptimo, GR(f) debe estar adaptado al pulso con espectro GT(f), por lo que |GR(f)|=|GT(f)|. Por ello, si el espectro del pulso recibido GT(f)GR(f) debe ser de la forma del coseno alzado, entonces, |GR(f)|=|GT(f)|=\/¯(coseno alzado). Sin embargo, la respuesta del canal nunca será plana, por lo que habrá que añadir un ecualizador que deshaga el efecto de la atenuación del canal para las distintas frecuencias. Por ejemplo, si el efecto de la atenuación del canal fuera proporcional a la raíz cuadrada de la frecuencia, añadiríamos un ecualizador cuya ganancia fuera proporcional a la raíz cuadrada de la frecuencia también. El problema de realizar éso es que el ecualizador refuerza las altas componentes frecuenciales del ruido, que pueden enmascarar a las altas componentes frecuenciales de la señal. Para evitarlo se ensalzan las altas componentes frecuenciales de la señal transmitida desde el transmisor (algo similar a las técnicas de pre- y de-énfasis).

7. Implementación del filtro adaptado

Las características del filtro adaptado han surgido bajo la suposición de que la ISI es despreciable. Hemos visto también que los pulsos en coseno alzado cumplen ese criterio. Ya que el espectro frecuencial de esos pulsos es real, tanto el transmisor como el receptor deben tener una respuesta en fase lineal. Para implementar nuestro filtro podríamos elegir cualquiera de los tipos existentes (FIR, IIR o analógicos). Sin embargo los IIR muestran unos retrasos no lineales a lo largo de la banda frecuencial que nos conducirían a tener ISI. Por otra parte, si bien con los analógicos sucede lo mismo, éstos pueden ser complementados con un ecualizador que cancele la no linealidad de dichos retardos. Como todo en el mundo tiende a la digitalización, dejaremos a un lado los filtros analógicos y emplearemos los filtros FIR digitales, ya que son además los que mejor se adecúan a nuestros requisitos, ya que los FIR con coeficientes simétricos cumplen bien los requerimientos de fase lineal y los retardos no constituyen un problema.

8. Ptolemy y sus filtros y pulsos adaptados.

Dentro del dominio SDF hay una galaxia denominada Signal processing que incluye numerosos filtros (FIR, IIR y de otros tipos que yo de momento desconozco), ademas de algunas operaciones como la convolucion y el desplazamiento de fases. Ademas hay una serie de estrellas agrupadas bajo el nombre de Filtros adaptativos que creo que nos pueden ser de gran utilidad para simular nuestro modem. Ademas, en el Ptolemy del bips78 hay alguna estrella nueva, como la del coseno alzado. Voy a intenar explicar las estrellas mas utiles:

FIR: Los coeficientes del FIR se determinan en el parametro taps. Los parametros por defecto constituyen un filtro paso-bajo de orden 8 y con fase lineal. Ademas dichos coeficientes se pueden sacar de un fichero. Esta estrella permite ademas la simulacion de sitemas multirate y para ello añade parametros como los factores de interpolacion y de diezmado. Ademas de esta estrella Ptolemy tambien dispone de las estrellas FIRCx y FIRFix, teniendo estos coeficientes complejos o de punto fijo.

Coseno alzado: Es un filtro FIR con una respuesta frecuencial en coseno alzado. Esta estrella tambien se encuentra en la galaxia Communications, ademas de un filtro en coseno alzado para entradas complejas.

LMS: Es un filtro adaptativo que utiliza el algoritmo de adaptacion del menor error cuadratico (no se muy bien como se traduce Least-Mean Square). Sus parametros vuelven a ser los parametros del filtro y por defecto son los de un paso bajo de orden 8. Esta estrella es una derivada de la estrella FIR, pero no soporta interpolacion (aunque si diezmado). Para utilizar esta estrella habria que comparar la salida del filtro con una señal de referencia para producir una señal de error. La señal de error la realimentariamos a la entrada. Uno de los parametros que hay que introducir es el retraso entre la salida del filtro y la entrada de errores. El numero de retrasos debe ser mayor que cero para que no se produzcan deadlocks. Ademas de esta estrella hay otras como LMSCx, LMSCxTKPLOT, etc, que permiten trabajar con complejos, representar los coeficientes del filtro y disponer de controles asociados, etc.

Ademas de estas estrellas, tenemos otras que podrian ser de interes, como BlockFIR, que permite recalcular los coeficientes de un fir periodicamente con alguna informacion exterior.

Dentro de la galaxia Communications tenemos una serie de estrellas para modelar diferentes canales: Canales con AWGN, canales ruidosos, canales con offset de fase, canales con distorsion no lineal y canales telefonicos. (Estas estrellas tambien se encuentran en la galaxia Telecommunications).

En una de las demos, dentro de l apartado de Signal processing hay una demo bastante interesante que se puede parecer a lo que tengamos que hacer, ya que simula un filtro adaptado: utiliza una señal gaussiana que introduce a un FIR y a un LMS, haciendo la comparacion entre ambas.